# Problem Statement There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer `n`, indicating that you must do the following routine for `n` minutes: - At the first minute, color **any** arbitrary unit cell blue. - Every minute thereafter, color blue **every** uncolored cell that touches a blue cell. Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.  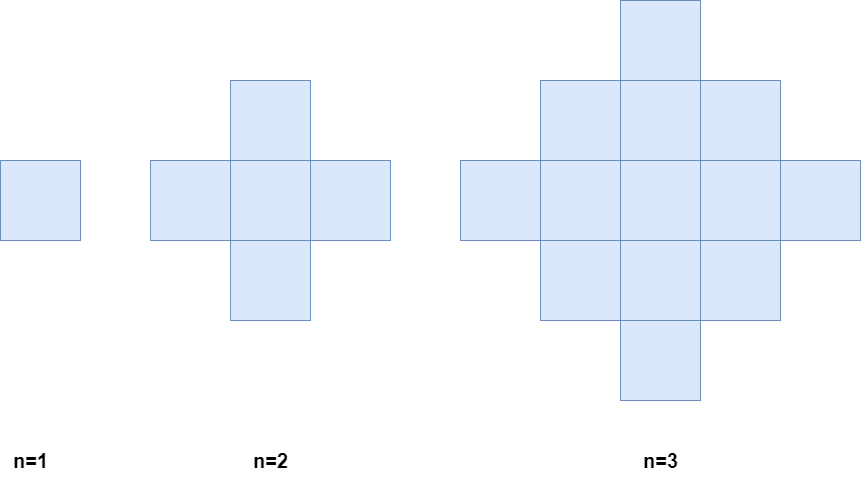Return _the number of **colored cells** at the end of_ `n` _minutes_. ## Constraints - `1 <= n <= 10^5` # Solution Solving this problem just requires us to construct a closed-form formula. My solution uses the observation that for each half of the diamond we can use half of that half to make a square. Since we always have an odd number of rows and columns these halves won't be perfect halves, but we can solve the problem regardless. ![[Pasted image 20250307140018.png]] ```python return n**2 + (n-1)**2 ``` Time Complexity: O$(1)$ | Space Complexity: O$(1)$